Contract as Automaton: The Computational Representation of Financial Agreements

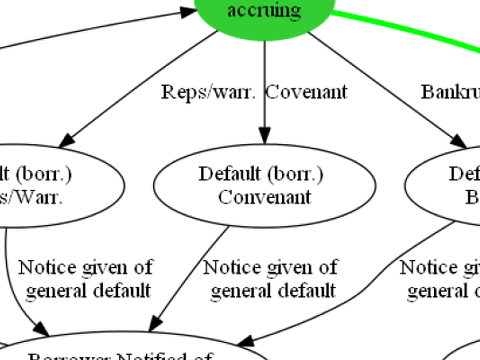
This paper shows that the fundamental legal structure of a well-written financial contract follows a logic that can be formalized mathematically as a "deterministic finite automaton." This allows, for example, automated reasoning to determine whether a contract is internally coherent and complete. The paper illustrates the process by representing a simple loan agreement as an automaton. (Working Paper no. 15-04)

Abstract

We show that the fundamental legal structure of a well-written financial contract follows a state-transition logic that can be formalized mathematically as a finite-state machine (specifically, a deterministic finite automaton or DFA). The automaton defines the states that a financial relationship can be in, such as “default,” “delinquency,” “performing,” etc., and it defines an “alphabet” of events that can trigger state transitions, such as “payment arrives,” “due date passes,” etc. The core of a contract describes the rules by which different sequences of events trigger particular sequences of state transitions in the relationship between the counterparties. By conceptualizing and representing the legal structure of a contract in this way, we expose it to a range of powerful tools and results from the theory of computation. These allow, for example, automated reasoning to determine whether a contract is internally coherent and whether it is complete relative to a particular event alphabet. We illustrate the process by representing a simple loan agreement as an automaton.

Keywords: Financial contracting, state-transition system, deterministic finite automaton, theory of computation, contractual complexity
JEL codes: D86, K12, C63