Hedging Market Risk in Optimal Liquidation

This paper discusses optimal strategies for financial institutions in selling large blocks of securities and in hedging the resulting market risk. (Working Paper no. 14-08)

Abstract

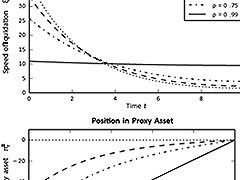
Financial institutions commonly face the risk that large trades will execute at unfavorable prices due to price impact effects from insufficient market liquidity. A typical method to manage these price impact effects is to split a given order into smaller pieces and to trade these pieces sequentially over time. Such a strategy, however, is exposed to market risk. Unlike price impact,market risk can be hedged. This paper explores the market risk management of the liquidation of a large trade that is subject to price impact. Specifically, we consider an investor, such as a large financial institution or a broker-dealer, who must a priori liquidate a large position in a primary risky asset whose price is influenced by the investor’s liquidation strategy. The investor hedges the market risk involved with liquidation by simultaneously taking a position in a liquid proxy asset that is imperfectly correlated with the primary asset. We show that the optimal strategies for an investor with a finite investment horizon and constant absolute risk aversion are deterministic and we find them explicitly using the calculus of variations. We find that the liquidation strategy for an investor able to hedge market risk is the same as the liquidation strategy of a less risk-averse investor without such a hedge. Similarly, the liquidation strategy for an investor able to hedge market risk is the same as for an investor facing higher price impact effects but without the ability to hedge market risk.

Keywords: optimal liquidation, optimal execution, hedging market risk, block trades, indifference price, price spread